O puzzle de uma manta de retalhos: Parte 1
Triângulos, rectângulos, números
Antes de começar, devo avisar os leitores habituais deste blog que os próximos dois posts vão divergir completamente do que geralmente escrevo por aqui. Zero tricô!
Já tenho vontade de costurar uma manta de retalhos desde que comecei a costurar (falei disso no podcast várias vezes). Sempre gostei muito do modelo de manta de retalhos Little Peaks Quilt da Purl Soho, mas depois de ler as instruções do modelo percebi que este modelo não se adapta bem à minha personalidade, porque não há nenhum plano para a utilização dos tecidos. Dizem apenas para escolher “dois triângulos” ao acaso, sem planeamento de cores.
A amostra da Purl Soho é linda:

No entanto, eu quero utilizar tecidos com cores muito diferentes e é difícil para mim começar um projecto desta magnitude sem ter a certeza de que vou gostar do resultado final.
Enquanto andava a ponderar a questão da manta de retalhos, fui à procura de tecidos e descobri que existem rolos de tiras de tecidos pré-cortados com cores concordantes. Queria utilizar cores neutras e uma cor contrastante. Acabei por escolher um rolo Robert Kaufman Kona Neutrals Palette 2-1/2" Roll-Up e 1 "fat quarter" extra na cor Kumquat.

O plano era seguir as instruções do modelo mencionado mais acima, mas seguir o meu esquema de cores, que ao contrário do modelo não iria ter uma cor que é repetida triângulo sim triângulo não.
Ao utilizar o rolo de tecido, iria ter 37 cores e o cor de laranja do “fat quarter”. De cada tira de tecido conseguia cortar 31 triângulos equiláteros de comprimento 6.35cm; do “fat quarter” também conseguia cortar pelo menos 31 triângulos iguais. No total iria ter 38 x 31 = 1178 triângulos. Agora teria de determinar a localização de cada triângulo, que poderiam estar colocados ao acaso, excepto que 2 triângulos da mesma cor nunca poderiam estar ao lado um do outro, tanto à esquerda como à direita, e tanto na fila acima como na fila abaixo. Os vértices dos triângulos não me preocupavam, apenas os lados dos triângulos.
|
Esta hipótese era aceitável:
|
Esta hipótese era o que queria evitar:
|
Ao ignorar os vértices, percebi que podia pensar em rectângulos em vez de triângulos e obter o mesmo resultado.
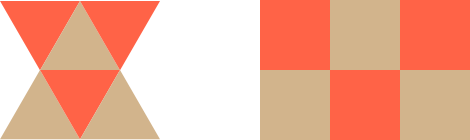
Os rectângulos simplificaram o problema e comecei a pensar em números em vez de cores. Podia procurar uma solução para números e atribuir uma cor a cada número mais tarde.
O próximo passo passou por determinar o comprimento e largura da manta de retalhos em termos de triângulos. Decidi que queria ter 22 triângulos de largura e 26 triângulos de altura, ou 139cm x 165cm (o resultado final vai ser sempre mais pequeno por causa margem de costura). Na verdade, as linhas horizontais de triângulos iriam utilizar o dobro dos triângulos que eu utilizei para determinar a largura da manta, e por isso iria utilizar 44 x 26 = 1144 triângulos no total.
Com esta informação o problema a resolver era este: organizar sequências de números de 1 a 38, numa matriz de [26 x 44], de forma a que cada número nunca seja repetido tanto para os lados como para as linhas acima e abaixo, e limitando a utilização de cada número a 31 vezes.
Desde o início senti que a forma mais rápida de resolver o problema seria com programação. O meu marido trabalha em informática e está sempre a tentar convencer-me a experimentar uma linguagem de programação que ele considera que me possa ser útil. Já me falou várias vezes de Racket particularmente porque facilmente se criam desenhos com esta linguagem de programação. Finalmente fui espreitar do que se tratava e a parte dos desenhos parecia ser bastante acessível (reparem nos desenhos bonitos que fiz mais acima). Mas antes de chegar à parte dos desenhos ainda tinha muito que fazer (tinha de comer muita sopa é o que me apetece escrever).
Para contextualizar a minha experiência com programação, tive uma cadeira de Introdução à Programação na faculdade onde trabalhámos com R e mais tarde participei num curso de Python no Coursera. Ou seja, não fazia ideia do que estava a fazer (e ainda não sei), mas tinha a sensação que um loop resolvia isto tudo. Claro que acabei por precisar muito da ajuda do meu marido, especialmente para ir de um vector para uma matriz. Nem o meu marido nem eu tínhamos qualquer experiência com Racket, por isso o código que escrevemos pode não estar escrito da forma mais idiomática.
(Estou com preguiça de traduzir os comentários 😓)
Preparativos:
;; dictionary that keeps track of the number of time a color was used
(define colors_count (make-hash))
;; maximum number of times a color can be used
(define MAX_COLOR_COUNT 31)
;; number of colors available
(define MAX_COLORS 38)
;; set all colors 1-38 to 31 available units on the dictionary
(for ([i MAX_COLORS])
(dict-set! colors_count i MAX_COLOR_COUNT))
;; start a vector 44 in length
(define row (build-vector 44 values))
;; first non colored row
(define NO_COLOR -1)
(define dummy (build-vector 44 (lambda (x) NO_COLOR)))
Seleccionar as cores tendo em conta a condição imposta:
;; pick a random color that still has available units on the dictionary
(define (random_color)
(let ([color (random (dict-count colors_count))])
(while #t
(set! color (random (dict-count colors_count)))
(let ([color_count (hash-ref colors_count color)])
(when (> color_count 0)
(break))))
color))
;; update the units available for each color
(define (updatedictionary color)
(dict-set! colors_count color (- (hash-ref colors_count color) 1)))
;; true if c1 is different from c2 and c3
(define (differ c1 c2 c3)
(and (not (equal? c1 c2))
(not (equal? c1 c3))))
;; select a color that is different from the previous selected color
;; and different from the color on the same index on the row below
(define (selectcolor previous_color below_color)
(if (and (equal? previous_color NO_COLOR) (equal? below_color NO_COLOR))
(begin
(updatedictionary (random_color))
(random_color))
;; else
(begin
;;continue looking for a color until it finds one that is different
;;from the previous color and the color on the same index on the row below
(let ([generated_color (random_color)])
(while (not (differ generated_color previous_color below_color))
(set! generated_color (random_color)))
(updatedictionary generated_color)
generated_color
))))
Criar a matriz e imprimir o resultado:
;; fills a vector with colors provided by the selectcolor function,
;; taking into account the colors on the row below
(define (paint_row below_row)
(let ([row (build-vector 44 values)])
(for ([i (vector-length row)])
(let ([below_color (vector-ref below_row i)])
;; for i=0, there isn't a previous color
(if (equal? i 0)
(begin
(vector-set! row i (selectcolor NO_COLOR below_color))
(display (~r (vector-ref row i) #:min-width 2 #:pad-string "0"))
(display " ")
)
;; else
;; looks for the previous color on index i-1 of vector row,
;; and selects a new color considering also the color below
(begin
(let ([previous_color (vector-ref row (- i 1))])
(let ([picked_color (selectcolor previous_color below_color)])
(display (~r picked_color #:min-width 2 #:pad-string "0"))
(display " " )
(vector-set! row i picked_color)
))))))row))
;; paints n rows and prints the result
(define (paint_n_rows n)
(let ([result (list)])
;; paints the first row and appends it to the result list
(let ([previous_row (paint_row dummy)])
(set! result (append result (list previous_row)))
(display "\n")
;; continues painting to n-1 and appends the results to the result list
(for ([i (- n 1)])
(begin
(set! previous_row (paint_row previous_row))
(set! result (append result (list previous_row)))
(display "\n")
)))
result))
Ao ler o código e escrever os comentários apercebi-me que só escrevi talvez metade do código. Sem a ajuda do meu marido ainda aqui estava a tentar escrever isto.
Mas aqui estamos com o assunto resolvido, e para por exemplo (paint_n_rows 4) o resultado é este:
31 36 33 29 28 02 11 12 33 15 03 08 30 02 37 11 21 26 19 36 27 11 09 07 15 09 14 35 26 36 12 19 21 24 12 20 30 34 32 30 14 15 26 29
11 04 07 00 06 14 17 06 14 12 37 24 21 30 31 25 29 15 25 03 07 01 14 03 14 36 24 08 33 17 02 24 02 08 00 01 02 03 08 24 10 07 32 33
34 17 13 07 33 20 13 18 26 16 06 36 10 32 25 00 12 09 16 07 26 22 01 14 02 27 10 13 22 16 17 13 37 23 30 02 11 24 28 16 01 17 29 01
19 29 37 18 37 30 04 32 21 11 24 34 21 16 20 26 17 26 18 28 33 09 10 12 19 23 12 37 01 33 08 03 11 01 23 28 00 03 32 12 13 24 02 04
A parte difícil estava feita e podia finalmente começar a brincar com os triângulos.
Como este post está enorme, isto é a Parte 1. Vou continuar na Parte 2.



