Before we get to the meat of the matter, followers of this blog beware: the next couple of posts will be different than what I usually share on this space, and will contain no knitting whatsoever.

I have wanted to make a quilt ever since I started sewing and Purl Soho’s Little Peaks Quilt pattern was exactly the sort of quilt that I was looking for. The only problem with the pattern is that there isn’t exactly a color plan before you start sewing, and you are expected to pick “any 2 triangles” at random.

Their sample is absolutely beautiful:

However I wanted to use very different colored fabrics and I would never start such a large project without making sure that I would like my version.

While I was still playing around with the idea of making a quilt, I went looking for fabric and discovered that you can buy strips of pre-cut fabric in a big roll of matching colors! I was looking for dark and mute colors, with a pop of color. I ended up selecting a Robert Kaufman Kona Neutrals Palette 2-1/2" Roll-Up and 1 extra fat quarter in the color Kumquat.

The plan was to follow the instructions for the pattern mentioned above, but to follow my own color scheme, which as opposed to the original pattern doesn’t have one solid color that gets repeated every other triangle.

Instead I would have 37 colors from the roll up, plus the orange. Each color/strip of the pre-cut fabric would yield 31 equilateral triangles of 6.35cm in length; the orange fat quarter would also yield at least 31 triangles of the same size. So in total I would have 38 x 31 = 1178 triangles. Now I would have to determine the placement of each different colored triangle, in no specific order, except that I didn’t want to have 2 triangles of the same color sewn next to each other (neither to the sides nor on the row above or below). I didn’t care about the vertices, only the sides.

Since I was ignoring the vertices, I realized that I could think in terms of rectangles and achieve the same result.

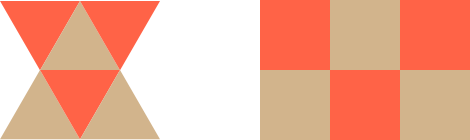
The rectangles simplified everything in mind and the next logical step was to think in numbers instead of colors. I would look for a solution in numbers and attribute a color to each number later on.

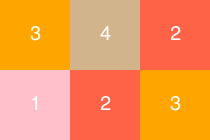
The next step was to determine the width and length of the quilt in triangles. I decided to have 22 triangles in width and 26 in height, or about 139cm x 165cm (after sewing it will be smaller than this due to the seam allowances). But the horizontal lines of triangles would actually use double the amount of triangles needed to determine the width, so I would need 44 x 26 = 1144 triangles in total.

With this information the problem I was trying to solve turned out to be: arrange sequences of numbers 1 to 38, in a matrix of [26 x 44], so that each number is never repeated either to the sides or in the rows above or below, and so that each number is never used more than 31 times.

From the beginning I felt that the easiest way to solve this would be with programming. My husband works in IT and from time to time tries to convince me to try a programming language that he thinks would suit me. He had been raving about Racket for a while, because I could draw stuff with it. I finally looked it up and the drawing aspect of it did seem pretty straight forward (notice the pretty drawings above). But I had some work to do before getting to the drawing bit.

As for my programming experience, I attended a course in Introduction to Programming in college where we worked in R and later I took a class in Python on Coursera. So I had no idea what I was doing (still don’t), but just had a vague idea that making a loop somehow would solve the problem. Let’s just say that my husband was a huge help, specially for going from one vector to a matrix. Neither my husband nor I had any experience with Racket, so this might not be the most idiomatic code.

Setting it up:

;; dictionary that keeps track of the number of time a color was used
(define colors_count (make-hash))

;; maximum number of times a color can be used
(define MAX_COLOR_COUNT 31)

;; number of colors available 
(define MAX_COLORS 38) 

;; set all colors 1-38 to 31 available units on the dictionary
(for ([i MAX_COLORS]) 
(dict-set! colors_count i MAX_COLOR_COUNT))

;; start a vector 44 in length 
(define row (build-vector 44 values)) 

;; first non colored row
(define NO_COLOR -1)
(define dummy (build-vector 44 (lambda (x) NO_COLOR)))

Work on picking colors making sure our condition is met:

;; pick a random color that still has available units on the dictionary
(define (random_color) 
  (let ([color (random (dict-count colors_count))]) 
    (while #t
           (set! color (random (dict-count colors_count))) 
           (let ([color_count (hash-ref colors_count color)]) 
             (when (> color_count 0) 
                 (break))))
    color))

;; update the units available for each color 
(define (updatedictionary color) 
   (dict-set! colors_count color (- (hash-ref colors_count color) 1)))

;; true if c1 is different from c2 and c3
(define (differ c1 c2 c3) 
  (and (not (equal? c1 c2))
       (not (equal? c1 c3))))

;; select a color that is different from the previous selected color 
;; and different from the color on the same index on the row below
(define (selectcolor previous_color below_color) 
  (if (and (equal? previous_color NO_COLOR) (equal? below_color NO_COLOR))
      (begin
        (updatedictionary (random_color))
        (random_color))
      ;; else
      (begin
        ;;continue looking for a color until it finds one that is different
        ;;from the previous color and the color on the same index on the row below
        (let ([generated_color (random_color)])
          (while (not (differ generated_color previous_color below_color)) 
                 (set! generated_color (random_color)))
              (updatedictionary generated_color)
              generated_color
              ))))

Create the matrix and print the result:

;; fills a vector with colors provided by the selectcolor function, 
;; taking into account the colors on the row below 
(define (paint_row below_row)
  (let ([row (build-vector 44 values)])
    (for ([i (vector-length row)]) 
      (let ([below_color (vector-ref below_row i)])
        ;; for i=0, there isn't a previous color 
        (if (equal? i 0)
            (begin
              (vector-set! row i (selectcolor NO_COLOR below_color))
              (display (~r (vector-ref row i) #:min-width 2 #:pad-string "0"))
              (display " ")
              )
            ;; else
            ;; looks for the previous color on index i-1 of vector row, 
            ;; and selects a new color considering also the color below
            (begin
              (let ([previous_color (vector-ref row (- i 1))])
                (let ([picked_color (selectcolor previous_color below_color)]) 
                  (display (~r picked_color #:min-width 2 #:pad-string "0"))
                  (display " " )
                  (vector-set! row i picked_color)  
                  ))))))row))

;; paints n rows and prints the result 
(define (paint_n_rows n)
  (let ([result (list)]) 
    ;; paints the first row and appends it to the result list
  (let ([previous_row (paint_row dummy)]) 
    (set! result (append result (list previous_row)))
    (display "\n")
    ;; continues painting to n-1 and appends the results to the result list
    (for ([i (- n 1)]) 
      (begin
        (set! previous_row (paint_row previous_row)) 
        (set! result (append result (list previous_row)))
        (display "\n")
        )))
    result))

While going through the code and writing the comments for this post, I realized that I probably only wrote half of it. Without the help of my husband it would have taken me weeks or months to figure this out.

But here we are and, for example, the result of (paint_n_rows 4) looks like this:

31 36 33 29 28 02 11 12 33 15 03 08 30 02 37 11 21 26 19 36 27 11 09 07 15 09 14 35 26 36 12 19 21 24 12 20 30 34 32 30 14 15 26 29

11 04 07 00 06 14 17 06 14 12 37 24 21 30 31 25 29 15 25 03 07 01 14 03 14 36 24 08 33 17 02 24 02 08 00 01 02 03 08 24 10 07 32 33

34 17 13 07 33 20 13 18 26 16 06 36 10 32 25 00 12 09 16 07 26 22 01 14 02 27 10 13 22 16 17 13 37 23 30 02 11 24 28 16 01 17 29 01

19 29 37 18 37 30 04 32 21 11 24 34 21 16 20 26 17 26 18 28 33 09 10 12 19 23 12 37 01 33 08 03 11 01 23 28 00 03 32 12 13 24 02 04

Now that the hard part was done, I could finally start messing around with coloring triangles in Racket.

This post is getting huge, so this is Part 1. I will continue on Part 2.